Stability Again

The stable Farmer

In his book, My Old Boat Shop,WestonFarmer observed that he had discovered a rule of thumb target for comfort at sea and that was the pounds per square foot loading of the waterplane. He surmised that the optimum loading was 64 pounds per square foot of the waterplane, or to put it another way the underwater volume should be the area of the waterplane times 1 foot. He theorized that this would make the vessel the same weight as the sea surrounding it and thus the vessel would move with the sea not out of sync with it as would a lighter or heavier vessel. But what about the stability of such a vessel?

This idea intrigued me so I did some follow up. To dissect this theory we'll use a closed box 10' long by 4' wide and 2' deep. In the first iteration the box weighs 64 lbs per cubic foot or 128lbs per sqft of waterplane.

The green line is the waterline, the centre of gravity and the centre of buoyancy coincide. Logic tells you that this arrangement would not be very stable as it would rotate about the centres completely underwater. Add some sides,

Stability increases but comfort doesn't as the boat would move out of sync with the movement of the water. A wave passing through would start the boat moving upwards but not at the speed of the wave. As the wave passed and the trough arrived the boat would continue upwards due to inertia and then start to fall as the next wave arrived creating a very uncomfortable motion.

So what would happen if we loaded the boat as Mr. Farmer suggests?

Here it is,

Mr. Farmer's theory is that this loading would be very comfortable as the boat would move in sync with the water, Stability is much improved as the centre of bouyancy is now below the center of gravity and would move outboard as the boat heeled. Let's take a look at how that would work.

Here is our box boat at 40 degrees of heel,

However the immersed volume is too great so we must adjust the waterline (WL) and then determine the center of buoyancy, which is a piece of cake with a triangle.

You all remember your basic geometry of course. From that we can determine the metacentric height for that angle of heel and the righting arm.

But what did I discover? Here it is - If you look at the diagram above where we found the center of the triangle you'll notice that the line from the top left to the middle of the right side cuts though the deck line exactly in the centre, from that we can deduce that the center of buoyancy falls on a line joining the mid points of the two parallel sides. But where on that line?

Jim Michalak in a post here,  http://www.jimsboats.com/1dec15.htm shows you how to find the centre of effort of a four sided sail, that same method can be used with the above knowledge to find the center of buoyancy of a four sided immersed section but without the math. Here we go.

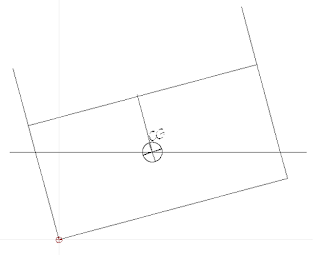
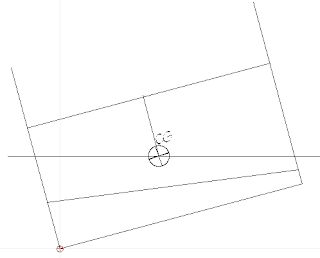
Here's our boat at 15 degrees of heel, the immersed volume is four sided.

First we join the two mid points,

Then divide the four sided figure into two triangles, find the centre of each and join the two centres.

Where the two lines joining centres and midpoints cross is the center of buoyancy.

But will it work for boats that don't have two parallel sides or a round bottom boats. Next time.